Трансляция арифметических выражений

Одной из важнейших задач при генерации кода является распределение регистров. Рассмотрим хорошо известную технику распределения регистров при трансляции арифметических выражений,

называемую алгоритмом Сети-Ульмана. (Замечание: в целях большей наглядности, в данном параграфе мы немного отступаем от семантики арифметических команд MC68020 и предполагаем, что команда

Op Arg1, Arg2

выполняет действие Arg2:=Arg1 Op Arg2.)

Пусть система команд машины имеет неограниченное число универсальных регистров, в которых выполняются арифметические команды. Рассмотрим, как можно сгенерировать код, используя для данного арифметического выражения минимальное число регистров.

Рис. 9.5:

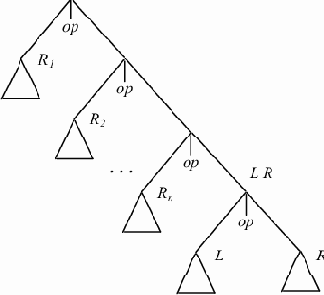
Пусть имеется синтаксическое дерево выражения. Предположим сначала, что распределение регистров осуществляется по простейшей схеме сверху-вниз слева-направо, как изображено на рис. 9.5. Тогда к моменту генерации кода для поддерева LR занято n регистров. Пусть поддерево L требует nl

регистров, а поддерево R - nr регистров. Если nl = nr, то при вычислении L будет использовано nl регистров и под результат будет занят (n + 1)-й регистр. Еще nr(= nl) регистров будет использовано

при вычислении R. Таким образом, общее число использованных регистров будет равно n + nl + 1.

Если nl > nr, то при вычислении L будет использовано nl регистров. При вычислении R будет использовано nr < nl регистров, и всего будет использовано не более чем n+nl регистров. Если nl < nr, то после вычисления L под результат будет занят один регистр (предположим, (n + 1)-й) и nr

регистров будет использовано для вычисления R. Всего будет использовано n+nr+1 регистров.

Видно,

что для деревьев, совпадающих с точностью до порядка потомков каждой вершины, минимальное число регистров при распределении их слева-направо достигается на дереве, у которого в каждой вершине слева расположено более «сложное» поддерево, требующее большего числа регистров. Таким образом, если дерево таково, что в каждой внутренней вершине правое поддерево требует меньшего числа регистров, чем левое, то, обходя дерево слева направо,

можно оптимально распределить регистры. Без перестройки дерева это означает, что если в некоторой вершине дерева справа расположено более сложное поддерево, то сначала сгенерируем код для него, а затем уже для левого поддерева.

Алгоритм работает следующим образом. Сначала осуществляется разметка синтаксического дерева по следующим правилам.

Правила разметки:

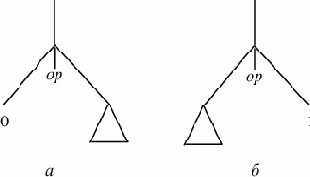
1) если вершина - правый лист или дерево состоит из единственной вершины, помечаем

эту вершину числом 1, если вершина - левый лист, помечаем ее 0 (рис. 9.6).

Рис. 9.6:

2) если вершина имеет прямых потомков с метками l1 и l2, то в качестве метки этой вершины выбираем наибольшее из чисел l1

или l2 либо число l1 + 1, если l1 = l2 (рис. 9.7).

Рис. 9.7:

Эта разметка позволяет определить, какое из поддеревьев требует большего количества регистров для своего вычисления. Далее осуществляется распределение регистров для результатов операций по следующим правилам:

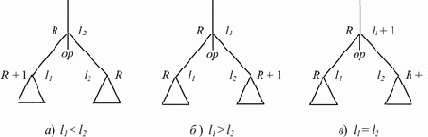
1) Корню назначается первый регистр.

2) Если метка левого потомка меньше метки правого, то левому потомку назначается регистр на единицу больший, чем предку, а правому - с тем же номером (сначала вычисляется правое

поддерево и его результат помещается в регистр R), так что регистры занимаются последовательно. Если же метка левого потомка больше или равна метке правого потомка, то наоборот, правому потомку назначается регистр на единицу больший, чем предку, а левому - с тем же номером (сначала вычисляется левое поддерево и его результат помещается в регистр R - рис. 9.7).

После этого формируется код по следующим правилам:

1) если вершина

- правый лист с меткой 1, то ей соответствует код

MOVE X, R

где R - регистр, назначенный этой вершине, а X - адрес переменной, связанной с вершиной (рис. 9.8, б);

Рис. 9.8:

2) если вершина внутренняя и ее левый потомок - лист с меткой 0, то ей соответствует код

Код правого поддерева     Op X, R

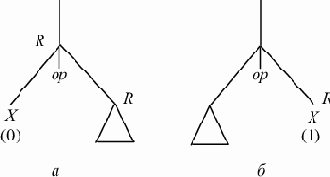
где R - регистр, назначенный этой вершине, X - адрес переменной, связанной с вершиной, а Op - операция, примененная в вершине (рис. 9.8, а);

3) если непосредственные потомки вершины не листья и метка правой вершины больше метки левой, то вершине соответствует код

Код правого поддерева      Код левого поддерева      Op R+1, R

где R - регистр, назначенный внутренней вершине, и операция Op, вообще говоря, не коммутативная (рис. 9.9, б);

Рис. 9.9:

4) если непосредственные потомки вершины не листья и метка правой вершины меньше или равна метке левой вершины, то вершине соответствует код

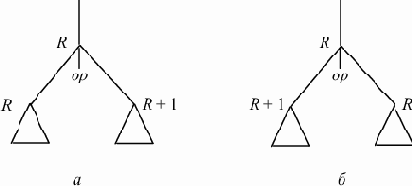
Код левого поддерева      Код правого поддерева      Op R, R+1      MOVE R+1, R

Последняя команда генерируется для того, чтобы получить результат в нужном регистре (в случае коммутативной операции операнды операции можно поменять местами и избежать дополнительной пересылки - рис. 9.9, а).

Рассмотрим атрибутную схему, реализующую эти правила генерации кода (для большей наглядности входная грамматика соответствует обычной инфиксной записи, а не Лидер-представлению). В этой

схеме генерация кода происходит не непосредственно в процессе обхода дерева, как раньше, а из-за необходимости переставлять поддеревья код строится в виде текста с помощью операции конкатенации. Практически, конечно, это нецелесообразно: разумнее управлять обходом дерева непосредственно, однако для простоты мы будем пользоваться конкатенацией.

RULE   Expr ::= IntExpr   SEMANTICS   Reg=1; Code=Code; Left=true.     RULE   IntExpr ::= IntExpr Op IntExpr   SEMANTICS   Left=true; Left=false;   Label=(Label==Label)            ? Label+1            : Max(Label,Label);   Reg=(Label )          ? Reg+1          : Reg;   Reg=(Label )          ? Reg          : Reg+1;   Code=(Label==0)           ? Code + Code             + Code + "," + Reg           : (Label )             ? Code + Code + Code +               (Reg+1) + "," + Reg             : Code + Code + Code +               Reg + "," + (Reg+1)               + "MOVE" + (Reg+1) + "," + Reg.     RULE   IntExpr ::= Ident   SEMANTICS   Label=(Left) ? 0 : 1;   Code=(!Left)           ? "MOVE" + Reg + "," + Val           : Val.     RULE   IntExpr ::= '(' IntExpr ')'   SEMANTICS   Label=Label;   Reg=Reg;   Code=Code.     RULE   Op ::= '+'   SEMANTICS   Code="ADD".     RULE   Op ::= '-'   SEMANTICS   Code="SUB".     RULE   Op ::= '*'   SEMANTICS   Code="MUL".     RULE   Op ::= '/'   SEMANTICS   Code="DIV".

<

Рис. 9.10:

Атрибутированное дерево для выражения A*B+C*(D+E) приведено на рис. 9.10. При этом будет сгенерирован следующий код:

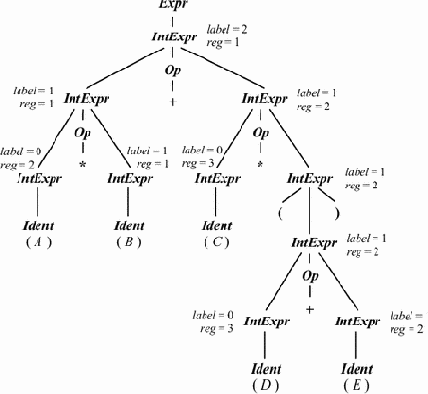
MOVE B, R1      MUL  A, R1      MOVE E, R2      ADD  D, R2      MUL  C, R2      ADD  R1, R2      MOVE R2, R1

Приведенная атрибутная схема требует двух проходов по дереву выражения. Рассмотрим теперь другую атрибутную схему, в которой достаточно одного обхода для генерация программы для выражений с оптимальным распределением регистров [7].

Пусть мы произвели разметку дерева разбора так же, как и в предыдущем алгоритме. Назначение

регистров будем производить следующим образом.

Левому потомку всегда назначается регистр, равный его метке, а правому - его метке, если она не равна метке его левого брата, и метке + 1, если метки равны. Поскольку более сложное поддерево всегда вычисляется раньше более простого, его регистр результата имеет больший номер, чем любой регистр, используемый при вычислении более простого поддерева, что гарантирует

правильность использования регистров.

Приведенные соображения реализуются следующей атрибутной схемой:

RULE   Expr ::= IntExpr   SEMANTICS   Code=Code; Left=true.     RULE   IntExpr ::= IntExpr Op IntExpr   SEMANTICS   Left=true; Left=false;   Label=(Label==Label)            ? Label+1            : Max(Label,Label);   Code=(Label > Label)           ? (Label==0)              ? Code + Code + Code                + "," + Label              : Code + Code + Code +                Label + "," + Label           : (Label )              ? Code + Code + Code +                Label + "," + Label +                "MOVE" + Label + "," + Label              : // метки равны                Code + "MOVE" + Label +                "," + Label+1 + Code +                Code + Label + "," +                Label+1.     RULE   IntExpr ::= Ident   SEMANTICS   Label=(Left) ? 0 : 1;   Code=(Left) ? Val           : "MOVE" + Val + "R1".     RULE   IntExpr ::= '(' IntExpr ')'   SEMANTICS   Label=Label;   Code=Code.     RULE   Op ::= '+'   SEMANTICS   Code="ADD".     RULE   Op ::= '-'   SEMANTICS   Code="SUB".     RULE   Op ::= '*'   SEMANTICS   Code="MUL".     RULE   Op ::= '/'   SEMANTICS   Code="DIV".

<


Команды пересылки требуются для согласования номеров регистров, в которых осуществляется выполнение операции, с регистрами, в которых должен быть выдан результат. Это имеет смысл, когда эти регистры разные. Получиться это может из-за того, что по приведенной

схеме результат выполнения операции всегда находится в регистре с номером метки, а метки левого и правого поддеревьев могут совпадать.

Для выражения A*B+C*(D+E) будет сгенерирован следующий код:

MOVE E, R1     ADD  D, R1     MUL  C, R1     MOVE R1, R2     MOVE B, R1     MUL  A, R1     ADD  R1, R2

В приведенных атрибутных схемах предполагалось, что регистров достаточно для трансляции любого выражения. Если это не так, приходится усложнять схему трансляции и при необходимости сбрасывать содержимое регистров в память (или магазин).


Содержание раздела

---

---