Синтаксический анализ для T-грамматик
Обычно код генерируется из некоторого промежуточного языка с довольно жесткой структурой. В частности, для каждой операции известна ее размерность, то есть число операндов, большее или равное 0. Операции задаются терминальными символами, и наоборот - будем считать все терминальные символы знаками операций. Назовем
грамматики, удовлетворяющие этим ограничениям, T-грамматиками. Правая часть каждой продукции в Т-грамматике есть правильное префиксное выражение, которое может быть задано следующим определением:
- Операция размерности 0 является правильным префиксным выражением;
- Нетерминал является правильным префиксным выражением;
- Префиксное выражение, начинающееся со знака операции размерности n > 0, является правильным, если после знака операции следует
n правильных префиксных выражений;
- Ничто другое не является правильным префиксным выражением.
Образцы, соответствующие машинным командам, задаются правилами грамматики (вообще говоря, неоднозначной). Генератор кода анализирует входное префиксное выражение и строит одновременно все возможные деревья разбора. После окончания разбора выбирается дерево с наименьшей стоимостью. Затем по этому единственному оптимальному дереву генерируется
код.
Для T-грамматик все цепочки, выводимые из любого нетерминала A, являются префиксными выражениями с фиксированной арностью операций. Длины всех выражений из входной цепочки a1...an можно предварительно вычислить (под длиной выражения имеется ввиду длина подстроки, начинающейся с символа кода операции и заканчивающейся последним символом, входящим в выражение для этой операции). Поэтому можно проверить, сопоставимо ли некоторое правило с подцепочкой ai...ak входной цепочки a1...an,
проходя слева-направо по ai...ak. В процессе прохода по цепочке предварительно вычисленные длины префиксных выражений используются для того, чтобы перейти от одного терминала к следующему терминалу, пропуская подцепочки, соответствующие нетерминалам правой части правила.
Цепные правила не зависят от операций, следовательно, их необходимо проверять отдельно.
Применение одного цепного правила может зависеть от применения другого цепного правила. Следовательно, применение
цепных правил необходимо проверять до тех пор, пока нельзя применить ни одно из цепных правил. Мы предполагаем, что в грамматике нет циклов в применении цепных правил. Построение всех вариантов анализа для T-грамматики дано ниже в алгоритме 9.1. Тип Titem в алгоритме 9.1 ниже служит для описания ситуаций (т.е. правил вывода и позиции внутри правила). Тип Tterminal - это тип терминального символа грамматики, тип Tproduction - тип для правила вывода.
Алгоритм 9.1
|
Tterminal a[n]; setofTproduction r[n]; int l[n]; // l[i] - длина a[i]-выражения Titem h; // используется при поиске правил, // сопоставимых с текущей подцепочкой // Предварительные вычисления Для каждой позиции i вычислить длину a[i]-выражения l[i]; // Распознавание входной цепочки for (int i=n-1;i>=0;i-){ for (каждого правила A -> a[i] y из P){ j=i+1; if (l[i]>1) // Первый терминал a[i] уже успешно сопоставлен {h=[A->a[i].y]; do // найти a[i]y, сопоставимое с a[i]..a[i+l[i]-1] {Пусть h==[A->u.Xv]; if (X in T) if (X==a[j]) j=j+1; else break; else // X in N if (имеется X->w in r[j]) j=j+l[j]; else break; h=[A->uX.v]; //перейти к следующему символу } while (j!=i+l[i]); } // l[i]>1 if (j==i+l[i]) r[i]=r[i] + { (A->a[i]y) } } // for по правилам A -> a[i] y // Сопоставить цепные правила while (существует правило C->A из P такое, что имеется некоторый элемент (A->w) в r[i] и нет элемента (C->A) в r[i]) r[i]=r[i] + { (C->A) }; } // for по i Проверить, принадлежит ли (S->w) множеству r[0]; |
Множества r[i] имеют размер O(|P|). Можно показать, что алгоритм
имеет временную и емкостную сложность O(n).
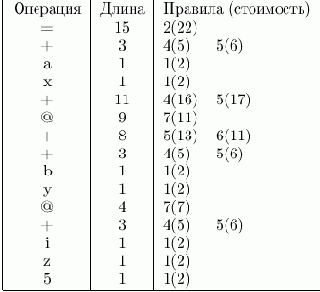
Рассмотрим вновь пример рис. 9.15. В префиксной записи приведенный фрагмент программы записывается следующим образом:
|
= + a x + @ + + b y @ + i z 5 |
|
PARSE. После обхода поддерева данной вершины в ней применяется процедура MATCHED, которая пытается найти все образцы, сопоставимые поддереву данной вершины. Для этого каждое правило-образец разбивается на компоненты в соответствии с встречающимися в нем операциями. Дерево обходится справа налево только для того, чтобы иметь соответствие с порядком вычисления в алгоритме 9.1. Очевидно, что можно обходить дерево вывода и слева направо.
Структура данных, представляющая
вершину дерева, имеет следующую форму:
|
struct Tnode { Tterminal op; Tnode * son[MaxArity]; setofTproduction RULEs; }; |
Алгоритм 9.2
|
Tnode * root; bool MATCHED(Tnode * n, Titem h) { bool matching; пусть h==[A->u.Xvy], v== v_1 v_2 ... v_m, m=Arity(X); if (X in T)// сопоставление правила if (m==0) // if l[i]==1 if (X==n->op) //if X==a[j] return(true); else return(false); else // if l[i]>1 if (X==n->op) //if X==a[j] {matching=true; for (i=1;i matching=matching && //while (j==i+l[i]) MATCHED(n->son[i-1],[A->uXv'.v_i v"y]); return(matching); //h=[A->uX.v] } else return(false); else // X in N поиск подвывода if (в n^.RULEs имеется правило с левой частью X) return(true); else return(false); } void PARSE(Tnode * n) { for (i=Arity(n->op);i>=1;i-) // for (i=n; i>=1;i-) PARSE(n->son[i-1]); n->RULEs=EMPTY; for (каждого правила A->bu из P такого, что b==n->op) if (MATCHED(n,[A->.bu])) //if (j==i+l[i]) n->RULEs=n->RULEs+{(A->bu)}; // Сопоставление цепных правил while (существует правило C->A из P такое, что некоторый элемент (A->w) в n->RULEs и нет элемента (C->A) в n->RULEs) n->RULEs=n->RULEs+{(C->A)}; } Основная программа // Предварительные вычисления Построить дерево выражения для входной цепочки z; root = указатель дерева выражения; // Распознать входную цепочку PARSE(root); Проверить, входит ли во множество root->RULEs правило с левой частью S; |
