Регулярные множества и их представления

В разделе 3.3.3 приведен алгоритм построения детерминированного конечного автомата по регулярному выражению. Рассмотрим теперь как по описанию конечного автомата построить регулярное множество, совпадающее с языком, допускаемым конечным автоматом.

Теорема3.1. Язык, допускаемый детерминированным конечным автоматом, является регулярным множеством.

Доказательство. Пусть L - язык допускаемый детерминированным

конечным автоматом M = ({q1, ..., qn}, T, D, q1, F). Введем De - расширенную функцию переходов автомата M: De(q, w) = p, где w

T*, тогда и только тогда, когда (q, w) *(p, e).

Обозначим Rijk множество всех слов x таких, что De(qi, x) = qj и если De(qi, y) = qs

для любой цепочки y - префикса x, отличного от x и e, то s

k.

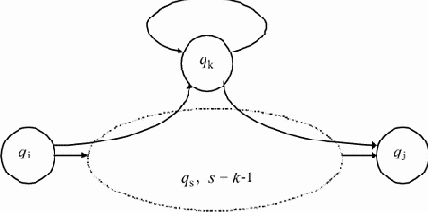
Иными словами, Rijk есть множество всех слов, которые переводят конечный автомат из состояния qi

в состояние qj, не проходя ни через какое состояние qs

для s > k. Однако, i и j могут быть больше k.

Rijk может быть определено рекурсивно следующим образом:

Rij0 = {a|a

T, D(qi, a) = qj},

Rijk = Rijk-1

Rikk-1(Rkkk-1)*Rkjk-1, где 1

k

n.

Таким образом, определение Rijk означает, что для входной цепочки w, переводящей M из qi в qj без перехода через состояния с номерами, большими k, справедливо ровно одно из следующих двух утверждений:

Цепочка w принадлежит Rijk-1, т.е. при анализе цепочки w автомат никогда не достигает состояний с номерами, большими или равными k.

Цепочка w может быть представлена в виде w = w1w2w3, где w1

Rikk-1 (подцепочка w1 переводит

M сначала в qk), w2

(Rkkk-1)* (подцепочка w2 переводит M из qk обратно в qk, не проходя через состояния с номерами, большими или равными k), и w3

Rkjk-1 (подцепочка w3 переводит M из состояния qk в qj) - рис. 3.16.

Рис. 3.16:

Тогда L =

qj

FR1jn. Индукцией по k можно показать, что это множество является регулярным. __

Таким образом, для всякого регулярного множества имеется конечный автомат, допускающий в точности это регулярное множество, и наоборот - язык, допускаемый конечным автоматом есть регулярное множество.

Рассмотрим теперь соотношение между языками, порождаемыми праволинейными грамматиками и допускаемыми конечными автоматами.

Праволинейная грамматика G = (N, T, P, S) называется регулярной,

если

• каждое ее правило, кроме S
  
  e, имеет вид либо A
  
  aB, либо A
  
  a, где A, B
  
  N, a
  
  T;



• в том случае, когда S
  
  e
  
  P, начальный символ S не встречается в правых частях правил.

Лемма. Пусть G - праволинейная грамматика. Существует регулярная грамматика G' такая, что L(G) = L(G').

Доказательство. Предоставляется читателю в качестве упражнения. __

Теорема 3.2. Пусть G = (N, T, P, S) - праволинейная грамматика. Тогда существует конечный автомат M = (Q, T, D, q0, F) для которого L(M) = L(G).

Доказательство. На основании приведенной выше леммы, без ограничения общности можно считать, что G - регулярная грамматика.

Построим недетерминированный конечный автомат M следующим образом:

• состояниями M будут нетерминалы G плюс новое состояние R, не принадлежащее N. Так что Q = N
  
  
  
  {R};



• в качестве начального состояния M примем S, т.е. q0 = S;



• если P содержит правило S
  
  
  
  e, то F = {S, R}, иначе F = {R}. Напомним, что S не встречается в правых частях правил, если S
  
  e
  
  P;



• состояние R
  
  D(A, a), если A
  
  a
  
  P. Кроме
  
  того, D(A, a) содержит все B такие, что A
  
  aB
  
  P. D(R, a) =
  
  для каждого a
  
  
  
  T.

M, читая вход w, моделирует вывод w в грамматике G. Покажем, что L(M) = L(G). Пусть w = a1a2...an L(G), n 1. Тогда

для некоторой последовательности нетерминалов A1, A2, ..., An-1. По определению, D(S, a1) содержит A1, D(A1, a2) содержит A2, и т.д., D(An-1, an) содержит R. Так что w L(M), поскольку De(S, w) содержит R, а R F. Если e L(G), то S F, так что e L(M).

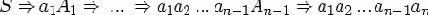
Аналогично, если w = a1a2...an L(M), n 1, то существует последовательность состояний S, A1, A2, ..., An-1, R такая, что

D(S, a1) содержит A1, D(A1, a2) содержит A2, и т.д. Поэтому



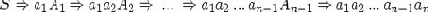
- вывод в G и x L(G). Если e L(M), то S F, так что S e P и e L(G). __

Теорема 3.3. Для каждого конечного автомата M = (Q, T, D, q0, F) существует праволинейная грамматика G = (N, T, P, S) такая, что L(G) = L(M).



Доказательство. Без потери общности можно считать, что автомат M - детерминированный. Определим грамматику G следующим образом:

• нетерминалами грамматики
  
  G будут состояния автомата M. Так что N = Q;



• в качестве начального символа грамматики G примем q0, т.е. S = q0;



• A
  
  aB
  
  P, если D(A, a) = B;



• A
  
  a
  
  P, если D(A, a) = B и B
  
  F;



• S
  
  e
  
  P, если q0
  
  F.

Доказательство того, что S *w тогда и только тогда, когда De(q0, w) F, аналогично доказательству теоремы 3.2. __


Содержание раздела

---

---