Основы конструирования компиляторов
          

Преобразователи с магазинной памятью


Рассмотрим важный класс абстрактных устройств, называемых преобразователями с магазинной памятью. Эти преобразователи получаются из автоматов с магазинной памятью, если к ним добавить выход и позволить на каждом шаге выдавать выходную цепочку.

Преобразователем с магазинной памятью (МП-преобразователем) называется восьмерка P = (Q, T,

Преобразователи с магазинной памятью
,
Преобразователи с магазинной памятью
, D, q0, Z0, F), где все символы имеют тот же смысл, что и в определении МП-автомата, за исключением

того, что

Преобразователи с магазинной памятью
- конечный выходной алфавит, а D - отображение множества QЧ(T
Преобразователи с магазинной памятью
{e})Ч
Преобразователи с магазинной памятью

в множество конечных подмножеств множества Q Ч

Преобразователи с магазинной памятью
*Ч
Преобразователи с магазинной памятью
*.

Определим конфигурацию преобразователя P как четверку (q, x, u, y), где q

Преобразователи с магазинной памятью
Q - состояние, x
Преобразователи с магазинной памятью
T* - цепочка на входной ленте, u
Преобразователи с магазинной памятью
Преобразователи с магазинной памятью
* - содержимое магазина, y
Преобразователи с магазинной памятью
Преобразователи с магазинной памятью
* - цепочка на выходной ленте, выданная вплоть до настоящего момента.

Если множество D(q, a, Z) содержит элемент (r, u, z), то будем писать (q, ax, Zw, y)

Преобразователи с магазинной памятью
(r, x, uw, yz) для любых x
Преобразователи с магазинной памятью
T*, w
Преобразователи с магазинной памятью
Преобразователи с магазинной памятью
* и y
Преобразователи с магазинной памятью
Преобразователи с магазинной памятью
*. Рефлексивно-транзитивное замыкание отношения
Преобразователи с магазинной памятью
будем обозначать
Преобразователи с магазинной памятью
*.

Цепочку y назовем

выходом для x, если (q0, x, Z0, e)

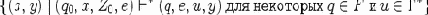
Преобразователи с магазинной памятью
*(q, e, u, y) для некоторых q
Преобразователи с магазинной памятью
F и u
Преобразователи с магазинной памятью
Преобразователи с магазинной памятью
*. Переводом (или трансляцией), определяемым МП-преобразователем P (обозначается
Преобразователи с магазинной памятью
(P)), назовем множество

Преобразователи с магазинной памятью

Будем говорить, что МП-преобразователь P является детерминированным (ДМП-преобразователем), если выполняются следующие условия:

  • для всех q
    Преобразователи с магазинной памятью
    Q, a
    Преобразователи с магазинной памятью
    T
    Преобразователи с магазинной памятью
    {e} и Z
    Преобразователи с магазинной памятью
    Преобразователи с магазинной памятью
    множество D(q, a, Z) содержит не более одного элемента,

  • если D(q, e, Z)
    Преобразователи с магазинной памятью
    Преобразователи с магазинной памятью
    ,

    то D(q, a, Z) =

    Преобразователи с магазинной памятью
    для всех a
    Преобразователи с магазинной памятью
    T.

    • Пример5.1. Рассмотрим перевод

    Преобразователи с магазинной памятью
    , отображающий каждую цепочку x
    Преобразователи с магазинной памятью
    {a, b}*$, в которой число вхождений символа a равно числу вхождений символа b, в цепочку y = (ab)n, где n - число вхождений a или b в цепочку x. Например,
    Преобразователи с магазинной памятью
    (abbaab$) = ababab.

    Этот перевод может быть реализован ДМП-преобразователем P = ({q0, qf}, {a, b, $}, {Z, a, b}, {a, b}, D, q0, Z, {qf}) c функцией переходов:

     

    D(q0, X, Z) = {(q0, XZ, e)}, X

    Преобразователи с магазинной памятью
    {a, b},

    D(q0, $, Z) = {(qf, Z, e)},

    D(q0, X, X) = {(q0, XX, e)}, X

    Преобразователи с магазинной памятью
    {a, b},

    D(q0, X, Y ) = {(q0, e, ab)}, X

    Преобразователи с магазинной памятью
    {a, b}, Y
    Преобразователи с магазинной памятью
    {a, b}, X
    Преобразователи с магазинной памятью
    Y .

     



    Содержание раздела



    Главная сайта