Обобщенные схемы синтаксически управляемого перевода

Расширим определение СУ-схемы, с тем чтобы выполнять

более широкий класс переводов. Во-первых, позволим иметь в каждой вершине дерева разбора несколько переводов. Как и в обычной СУ-схеме, каждый перевод зависит от прямых потомков соответствующей вершины дерева. Во-вторых, позволим элементам перевода быть произвольными цепочками выходных символов и символов, представляющих переводы в потомках. Таким образом, символы перевода могут повторяться или вообще отсутствовать.

Определение. Обобщенной схемой синтаксически управляемого перевода (или трансляции, сокращенно: OСУ-схемой) называется шестерка Tr = (N, T,

, , R, S), где все символы имеют тот же смысл, что и для СУ-схемы, за исключением того, что

• 
  - конечное множество символов перевода вида Ai, где A
  
  N и i - целое число;
• R - конечное множество правил перевода вида

  A

  
  u, A1 = v1, ..., Am = vm,

  удовлетворяющих следующим условиям:

• Aj
  
  
  для 1
  
  j
  
  m,
• каждый символ, входящий в v1, ..., vm, либо принадлежит
  
  , либо является Bk
  
  
  , где B входит в u,
• если u имеет более одного вхождения символа B, то каждый символ Bk

  во всех v соотнесен (верхним индексом) с конкретным вхождением B.

A

u называют входным правилом вывода, Ai - переводом нетерминала A, Ai = vi - элементом перевода, связанным с этим правилом перевода. Если в ОСУ-схеме нет двух правил перевода с одинаковым входным правилом вывода, то ее называют семантически однозначной.

Выход ОСУ-схемы определим снизу вверх. С каждой внутренней вершиной n дерева разбора (во входной грамматике), помеченной A, свяжем одну цепочку для каждого Ai. Эта цепочка называется значением (или переводом) символа Ai

в вершине n. Каждое значение вычисляется подстановкой значений символов перевода данного элемента перевода Ai = vi, определенных в прямых потомках вершины n.

Переводом

(Tr), определяемым ОСУ-схемой Tr, назовем множество {(x, y) | x имеет дерево разбора во входной

грамматике для Tr и y - значение выделенного символа перевода Sk в корне этого дерева}.

Пример 5.4.
Рассмотрим формальное дифференцирование выражений, включающих константы 0 и 1, переменную x, функции sin и cos , а также операции * и +. Такие выражения порождает грамматика

 

	E E + T | T
	T T * F | F
	F (E) | sin (E) | cos (E) | x | 0 | 1

 

Свяжем с каждым из E, T и F два перевода, обозначенных индексом 1 и 2. Индекс 1 указывает на то, что выражение не дифференцировано, 2 - что выражение продифференцировано. Формальная производная - это E2. Законы дифференцирования таковы:

d(f(x) + g(x)) = df(x) + dg(x)

d(f(x) * g(x)) = f(x) * dg(x) + g(x) * df(x)

d sin (f(x)) = cos (f(x)) * df(x)

d cos (f(x)) = - sin (f(x))df(x)

dx = 1

d0 = 0

d1 = 0

Эти законы можно реализовать следующей ОСУ-схемой:

 

E E + T	E1 = E1 + T1
	E2 = E2 + T2
E T	E1 = T1
	E2 = T2
T T * F	T1 = T1 * F1
	T2 = T1 * F2 + T2 * F1
T F	T1 = F1
	T2 = F2
F (E)	F1 = (E1)
	F2 = (E2)
F sin (E)	F1 = sin (E1)
	F2 = cos (E1) * (E2)
F cos (E)	F1 = cos (E1)
	F2 = - sin (E1) * (E2)
F x	F1 = x
	F2 = 1
F 0	F1 = 0
	F2 = 0
F 1	F1 = 1
	F2 = 0

 

Дерево вывода для sin(cos (x))+x приведено на рис. 5.1.

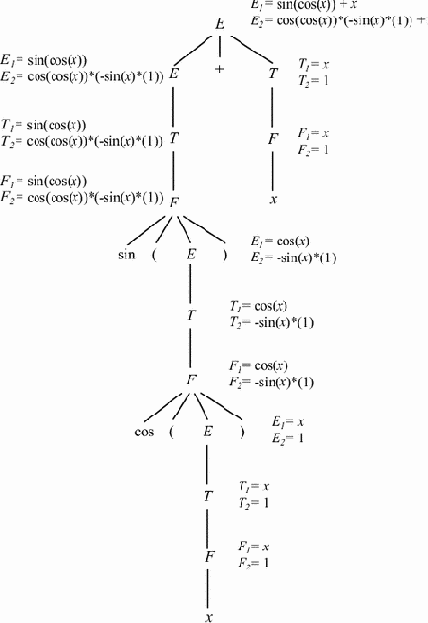
Рис. 5.1:

Содержание раздела

---

---