Конструирование LR(1)-таблицы
Рассмотрим теперь алгоритм конструирования таблицы, управляющей LR(1)-анализатором.
Пусть G = (N, T, P, S) - КС-грамматика. Пополненной грамматикой для данной грамматики G называется КС-грамматика
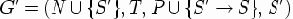

Это дополнительное правило вводится для того, чтобы определить, когда анализатор должен остановить разбор и зафиксировать допуск входа. Таким образом, допуск имеет место тогда и
только тогда, когда анализатор готов осуществить свертку по правилу S'

LR(1)-ситуацией называется пара [A






Будем говорить, что LR(1)-ситуация [A













Будем говорить, что ситуация допустима, если она допустима для какого-либо активного префикса.
Пример4.9. Рассмотрим
грамматику G = ({S, B}, {a, b}, P, S) с правилами
S  |
|
B  |
|
Существует правосторонний вывод S


raaaBab. Легко видеть, что ситуация [B







rBaaB. Поэтому для активного префикса Baa допустима ситуация [B

Центральная идея метода заключается в том, что по грамматике строится детерминированный конечный автомат, распознающий активные префиксы. Для этого ситуации группируются во множества, которые и образуют состояния автомата.
Ситуации можно рассматривать как состояния недетерминированного конечного автомата, распознающего активные префиксы, а их группировка на самом деле есть процесс построения детерминированного конечного автомата из недетерминированного.
Анализатор, работающий слева-направо по типу сдвиг-свертка, должен уметь распознавать основы на верхушке магазина. Состояние автомата после прочтения содержимого магазина и текущий входной символ определяют очередное действие автомата.
Функцией переходов этого конечного
автомата является функция переходов LR-анализатора. Чтобы не просматривать магазин на каждом шаге анализа, на верхушке магазина всегда хранится то состояние, в котором должен оказаться этот конечный автомат после того, как он прочитал символы грамматики в магазине от дна к верхушке.
Рассмотрим ситуацию вида [A









терминальная строка bw. Тогда для некоторого правила вывода вида B









выводится e в выводе



Система множеств допустимых LR(1)-ситуаций для всевозможных активных
префиксов пополненной грамматики называется канонической системой множеств допустимых LR(1)-ситуаций. Алгоритм построения канонической системы множеств приведен ниже.
Алгоритм 4.9. Конструирование канонической системы множеств допустимых LR(1)-ситуаций.
Вход. КС-грамматика G = (N, T, P, S).
Выход. Каноническая система C множеств допустимых LR(1)-ситуаций для грамматики G.
Метод. Заключается в выполнении для пополненной грамматики G' процедуры items, которая использует функции closure и goto.
function closure(I){ /* I - множество ситуаций */
do{
for (каждой ситуации [A



каждого правила вывода B


из G',
каждого терминала b из FIRST(

такого, что [B


добавить [B


}
while (к I можно добавить новую ситуацию);
return I;
}
function goto(I,X){ /* I - множество ситуаций;
X - символ грамматики */
Пусть J = {[A







return closure(J);
}
procedure items(G'){ /* G' - пополненная грамматика */
I0 = closure({[S'

C = {I0};
do{
for (каждого множества ситуаций I из системы C,
каждого символа грамматики X такого,
что goto(I, X) не пусто и не принадлежит C)
добавить goto(I, X) к системе C;
}
while (к C можно добавить новое множество ситуаций);
Если I - множество ситуаций, допустимых для некоторого активного префикса


Работа алгоритма построения системы C множеств допустимых
LR(1)-ситуаций начинается с того, что в C помещается начальное множество ситуаций I0 = closure({[S'

Рассмотрим теперь, как по системе множеств LR(1)-ситуаций строится LR(1)-таблица, т.е. функции действий и переходов LR(1)-анализатора.
Алгоритм 4.10. Построение LR(1)-таблицы.
Вход. Каноническая система C = {I0, I1, ..., In} множеств допустимых LR(1)-ситуаций для грамматики G.
Выход. Функции Action и Goto, составляющие LR(1)-таблицу для грамматики G.
Метод. Для каждого состояния i функции Action[i, a] и Goto[i, X] строятся по множеству ситуаций Ii:
- Значения функции действия (Action) для состояния i определяются следующим образом:
- если [A
 .a
.a , b]
, b] Ii (a - терминал) и goto(Ii, a) = Ij, то полагаем Action[i, a] = shift j;
Ii (a - терминал) и goto(Ii, a) = Ij, то полагаем Action[i, a] = shift j;
- если [A
 ., a]
., a] Ii, причем A
Ii, причем A S', то полагаем Action[i, a] = reduce A
S', то полагаем Action[i, a] = reduce A
 ;
;
- если [S'S., $]
 Ii, то полагаем Action[i, $] = accept.
Ii, то полагаем Action[i, $] = accept.
состояния i определяются следующим образом: если goto(Ii, A) = Ij, то Goto[i, A] = j (здесь A - нетерминал).

Таблица на основе функций Action и Goto, полученных в результате работы алгоритма 4.10, называется канонической LR(1)-таблицей.
LR(1)-анализатор, работающий с этой таблицей, называется каноническим LR(1)-анализатором.
Пример 4.10. Рассмотрим следующую грамматику, являющуюся пополненной для грамматики из примера 4.8:
(0) E' |
|
(1) E  |
|
(2) E  |
|
(3) T  |
|
(4) T  |
|
(5) F  |
|
Множества ситуаций и переходы по goto для этой грамматики приведены на рис. 4.11. LR(1)-таблица для этой грамматики приведена на рис. 4.9.

|
