Формальное определение грамматики

Для нас наибольший интерес представляет одна из систем генерации языков - грамматики. Понятие грамматики изначально было формализовано лингвистами при изучении естественных языков. Предполагалось, что это может помочь при их автоматической трансляции. Однако, наилучшие результаты в этом направлении достигнуты при описании не естественных языков, а языков программирования. Примером может служить способ описания синтаксиса языков

программирования при помощи БНФ - формы Бэкуса-Наура.

Определение. Грамматика - это четверка G = (N, T, P, S), где

• N - алфавит нетерминальных символов;
• T - алфавит терминальных символов, N
  
  T =
  
  ;
• P - конечное множество правил вида
  
  
  
  , где
  
  
  (N
  
  T)*N(N
  
  T)*,
  
  

  (N

  
  T)*;
• S
  
  N - начальный символ (или аксиома) грамматики.

Мы будем использовать большие латинские буквы для обозначения нетерминальных символов, малые латинские буквы из начала алфавита для

обозначения терминальных символов, малые латинские буквы из конца алфавита для обозначения цепочек из T* и, наконец, малые греческие буквы для обозначения цепочек из (N

T)*.

Будем использовать также сокращенную запись A

1|2|...|n для обозначения группы правил A 1, A 2, ..., A n.

Определим на множестве (N

T)* бинарное отношение выводимости следующим образом: если P, то

для всех

, (N T)*. Если 1 2, то говорят, что цепочка 2

непосредственно выводима из

1.

Мы будем использовать также рефлексивно-транзитивное и транзитивное замыкания

отношения

, а также его степень k 0 (обозначаемые соответственно *, + и k). Если 1 *2 (1 +2, 1 k2), то говорят, что цепочка 2 выводима (нетривиально выводима, выводима за k шагов) из 1.

Если

k (k 0), то существует последовательность шагов

где = 0 и = k. Последовательность цепочек 0, 1, 2, ..., k в этом случае называют выводом

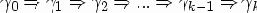
из

.

Сентенциальной формой грамматики G называется цепочка, выводимая из ее начального символа.

Языком, порождаемым грамматикой G (обозначается L(G)), называется множество всех ее терминальных сентенциальных форм, т.е.

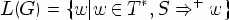
Грамматики G1

и G2 называются эквивалентными, если они порождают один и тот же язык, т.е.
L(G1) = L(G2).

Пример2.5. Грамматика G = ({S, B, C}, {a, b, c}, P, S), где

P = {S

aSBC, S aBC, CB BC, aB ab, bB bb, bC bc, cC cc}, порождает язык L(G) = {anbncn|n > 0}.

Действительно, применяем n- 1 раз правило 1 и получаем an-1S(BC)n-1, затем один раз правило 2 и получаем an(BC)n, затем n(n- 1)/2 раз правило 3 и

получаем anBnCn.

Затем используем правило 4 и получаем anbBn-1Cn. Затем применяем n- 1 раз правило 5 и получаем anbnCn. Затем применяем правило 6 и n - 1 раз правило 7 и получаем anbncn. Можно показать, что язык L(G) состоит из цепочек только такого вида.

Пример 2.6. Рассмотрим грамматику G = ({S}, {0, 1}, {S 0S1, S 01}, S). Легко видеть, что цепочка 000111 L(G), так как существует вывод



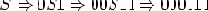
Нетрудно показать, что грамматика порождает язык L(G) = {0n1n|n > 0}.

Пример 2.7. Рассмотрим грамматику G = ({S, A}, {0, 1}, {S 0S,

S 0A, A 1A, A 1}, S). Нетрудно показать, что грамматика порождает язык L(G) = {0n1m|n, m > 0}.


Содержание раздела

---

---

---

Главная сайта

---