Операции над множествами
На базовом уровне отношения являются множествами. Следовательно, все операции над множествами являются допустимыми операциями реляционной алгебры. Операции над множествами применяются к отношениям, которые являются совместными по объединению. Два отношения совместны по объединению, если они содержат одинаковое количество столбцов, имеющих одинаковую область определения, и если столбцы расположены в одном и том же порядке слева направо.
-
Объединение. Если R и S есть отношения, то
возвращает все кортежи, которые встречаются или в R, или в S. Например, мы можем использовать операцию объединения для составления списка стран, которые либо расположены в Северной Америке, либо имеют реки, берущие исток на этом континенте.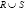
1.R = ?Name(?Cont=СА(Country)).
2. S = ?Origin(River).
3.
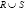
Результирующее отношение показано в таблице 3.4(а). Заметим, что атрибуты R.Name и S.Origin имеют общую область определения, поскольку атрибут R.Origin связан с Country.Name. Этого достаточно для того, чтобы отношения R и S были совместными по объединению.
- Пересечение. Для двух совместных по объединению отношений R и S оператор пересечения возвращает все кортежи, встречающиеся как в R, так и в S. Отметим, что эта операция, хотя и весьма удобна, является избыточной: ее можно получить из операции разности:
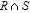 = R – (R – S). Чтобы найти все страны, которые расположены в Южной Америке и на территории которых находятся истоки рек, используем операцию пересечения. Результат представлен в таблице 3.4(в).
= R – (R – S). Чтобы найти все страны, которые расположены в Южной Америке и на территории которых находятся истоки рек, используем операцию пересечения. Результат представлен в таблице 3.4(в).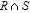
Векторное произведение. Эта операция применяется к любой паре отношений, а не только к отношениям, совместным по объединению. R x S возвращает отношение, схема которого содержит все атрибуты R, за которыми следуют все атрибуты S. Для простоты в таблице 3.3 приведен абстрактный пример этой операции. Обратите внимание на использование «точечной» нотации для различения атрибутов обоих отношений.
Разность. R – S возвращает все кортежи в R, которые отсутствуют в S. Оператор разности может использоваться, например, для отыскания всех стран в Северной Америке, на территории которых нет истоков рек (перечисленных в таблице River). Результирующее отношение показано в таблице 3.4(б).
1. R = ?Name(?Cont=СА(Country)).
2. S = ?Origin(River).
3. R – S.
1. R = ?Name(?Cont=ЮА(Country)).
2. S = ?Origin(River).
3.
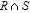
Таблица 3.3. Векторное произведение отношений R и S
| R | R.A | R.B |
| A1 | B1 | |
| A2 | B2 |
| S | S.C | S.D |
| C1 | D1 | |
| C2 | D2 |
| R ? S | R.A | R.B | S.C | S.D |
| A1 | B1 | C1 | D1 | |
| A1 | B1 | C2 | D2 | |
| A2 | B2 | C1 | D1 | |
| A2 | B2 | C2 | D2 |
Таблица 3.4. Результаты операций над множествами
| НАЗВАНИЕ |
| Канада |
| Мексика |
| Бразилия |
| Куба |
| США |
| НАЗВАНИЕ |
| Канада |
| Мексика |
| Куба |
| НАЗВАНИЕ |
| Бразилия |
