Классы алгоритмов

Одной из причин быстрого прогресса комбинаторных вычислений является усиление внимания к исследованию классов алгоритмов в противоположность изучению отдельных из них. Для того чтобы утверждать, например, что "все алгоритмы, предназначенные для выполнения того-то и того-то, должны обладать такими-то и такими-то свойствами" или "не существует алгоритма, удовлетворяющего тому-то и тому-то", необходимо иметь дело с четко определенным классом алгоритмов. Именно при таком определении становится возможным говорить, что данный алгоритм является оптимальным по отношению к некоторому свойству, если он работает по крайней мере так же хорошо (относительно этого свойства), как любой другой алгоритм из рассматриваемого класса.

Как можно строго определить, возможно, бесконечный, класс алгоритмов? Исследуем этот вопрос на примере задачи о фальшивой монете. Рассматриваемый в этом примере класс алгоритмов порождает более обширный и более важный класс алгоритмов - так называемые деревья решений.

Задача. Имеется

монет, о которых известно, что

из них являются настоящими и не более чем одна монета, фальшивая (легче или тяжелее остальных монет). Дополнительно к группе из

сомнительных монет дается еще одна монета, причем заведомо известно, что она настоящая. Имеются также весы, с помощью которых можно сравнить общий вес любых

монет с общим весом любых других

монет и тем самым установить, имеют ли две группы по

монет одинаковый вес либо одна из групп легче другой. Задача состоит в том, чтобы найти фальшивую монету, если она есть, за наименьшее число взвешиваний, или сравнений.

Решение Пусть сомнительные монеты занумерованы числами

. Монете, о которой известно, что она настоящая, поставим в соответствие номер 0. Пусть

- множество монет. Если

— непересекающиеся непустые подмножества множества

, то через

обозначим операцию сравнения весов множества

. При сравнении возможны три исхода, которые обозначим следующим образом:

в зависимости от того, является ли вес

меньшим, равным или большим веса

Рассматриваемые алгоритмы можно представить в форме дерева решений.

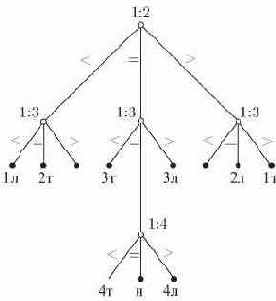
Рис. 1.1. Дерево решений для задачи о фальшивой монете с четырьмя монетами

Корень дерева на рисунке изображен полой окружностью и помечен отношением

. Это означает, что алгоритм начинает работу сравнением весов монет с номерами 1 и 2. Три исходящие из корня ветви ведут к поддеревьям, определяющим продолжение работы алгоритма после каждого из трех возможных исходов первого сравнения. Окружности, залитые черной краской, называются листьями дерева и означают, что работа алгоритма заканчивается. Метки соответствуют исходам: "1л" - монета 1 легкая, "1т" - монета 1 тяжелая, "н" - все монеты настоящие. Непомеченная вершина дерева означает, что при наших предположениях этот случай возникнуть не может.

Алгоритм, приведенный на рис. 1.1, требует двух сравнений в одних случаях и трех - в других. Скажем, что он требует "трех сравнений в худшем случае". Обычно важно знать, сколько работы требует алгоритм в среднем, однако для этого требуется задать вероятности различных исходов. Если предположим, что все девять исходов 1л, 1т, 2л, 2т, 3л, 3т, 4л, 4т, - равновероятны, то тогда этот алгоритм требует в среднем 7/3 сравнений.

На одну чашку весов можем положить больше одной монеты. Например, можно начать сравнения, положив на одну чашку весов монеты 1 и 2, а на другую - монеты 3 и 4 (рис. 1.2).

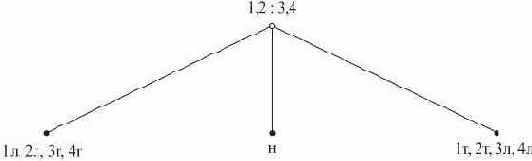
Рис. 1.2. Корень другого дерева решений для задачи о четырех монетах

Если посчастливится, задачу можно решить за одно сравнение - это может произойти, когда все монеты настоящие. Независимо от того, как дополняется это дерево решений, в худшем случае задача все равно потребует тех же трех сравнений, поскольку единственное тернарное решение не может идентифицировать один из четырех исходов, которые возможны на ветви, помеченной символом "

", так же как и один из четырех исходов на ветви, помеченной символом "

". К тому же, независимо от того, как дополняется это дерево решений, оно потребует в среднем по крайней мере 7/3 сравнений, и в этом случае оно не лучше, чем дерево на рис.1.1.

Используя монету 0, о которой известно, что она настоящая, можно получить приведенное на рис. 1.3 дерево решений (полное двухъярусное тернарное дерево), которое и в худшем, и в среднем случае требует двух сравнений.

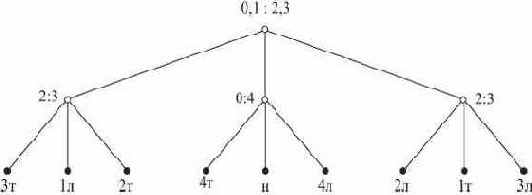
Рис. 1.3. Оптимальное дерево решений для задачи о четырех монетах

Рассматриваемый класс алгоритмов решения задачи о фальшивой монете есть множество тернарных деревьев решений (примеры на рис.1.1, рис.1.2,

рис.1.3), обладающих следующими свойствами:

каждый узел помечен сравнением
, где
и
- непересекающиеся непустые подмножества множества
всех монет;
каждый лист либо не помечен, что соответствует невозможному исходу в предположении существования не более чем одной фальшивой монеты, либо помечен одним из исходов iл, iT, н, означающим соответственно, что все монеты настоящие. Четко определив подлежащий дальнейшему рассмотрению класс алгоритмов, можно исследовать свойства, которыми должно обладать каждое дерево из этого класса, и определить, как найти алгоритмы, являющиеся в некотором смысле оптимальными. Решим эту проблему в начале для четырех монет, а затем перейдем к общему случаю.

Поскольку в задаче о четырех монетах требуется различить девять возможных исходов, любое дерево решений для этой задачи должно иметь, по крайней мере, девять листьев и, следовательно, не менее двух ярусов. Поэтому дерево на рис.1.3 является оптимальным и для худшего случая, и для среднего. Существуют ли другие оптимальные деревья? Для ответа на этот вопрос нужно рассмотреть множество всех деревьев решений для задачи о четырех монетах. Попытаемся исключить из дальнейшего рассмотрения какую-либо часть этого множества. Прежде всего видно, что путем любой перестановки множества

сомнительных монет из одного дерева, приведенного на рис.1.3, можно получить другие оптимальные деревья. Все они будут изоморфны дереву на рис.1.3. Исходя из этого, уточним постановку задачи и будем интересоваться попарно неизоморфными деревьями.

Рассмотрим затем, существует ли оптимальное дерево среди тех, у которых в корне не используется монета с номером n.

При таком ограничении в корне дерева можно сделать только два различных сравнения, а именно

. Рассмотрим разбиение исходов по трем ветвям, выходящим из корня, как показано на рис.1.2. Для получения такого, как на рис.1.3, полного двухъярусного тернарного дерева, девять возможных исходов должны были бы быть разбиты в отношении (3, 3, 3). Они же вместо этого разбиваются, соответственно, в отношении (2, 5, 2) и (4,1,4). Таким образом, заключаем, что задачу для четырех монет нельзя решить за два сравнения, не используя дополнительную настоящую монету.

Наконец, рассмотрим те деревья решений, которые используют монету 0 в корне. В этом случае видно, что в корне фактически возможны только два сравнения:

. Для первого сравнения набор исходов будет (1, 7, 1), в связи с чем все алгоритмы, начинающиеся таким способом, для нас непригодны. Набор исходов (3, 3, 3) приводит к оптимальному дереву, показанному на рис.1.3. Аналогичным образом устанавливается, что для оптимального дерева сравнения в первом от корня ярусе определяются единственным образом. Отсюда заключаем, что для задачи о четырех монетах фактически существует только одно оптимальное дерево.

Когда используемые идеи анализа задачи о четырех монетах переносятся на произвольный случай, в некоторой степени все идеи обобщаются на случай любого числа монет. Однако некоторые из них не имеют практического значения, когда

значительно больше четырех. В принципе, оптимальные деревья решений всегда можно найти путем систематического поиска в множестве деревьев, поскольку для любого заданного

в качестве кандидатов требуется рассмотреть лишь конечное число деревьев решений. В лекции обсуждается техника исчерпывающего поиска в таких конечных множествах. Однако, если даже поиск организован разумно и рассматриваются лишь существенно различные (не изоморфные) деревья, эта процедура не может служить практическим способом отыскания оптимальных деревьев решений. С ростом

число деревьев растет экспоненциально, и поэтому техника исчерпывающего поиска имеет практическое значение только для малых значений

.

Поскольку число листьев в дереве решений должно быть по крайней мере таким же, как и число возможных исходов задачи (

для задачи о монетах), сразу же можно получить нижнюю оценку необходимого числа сравнений (или, что эквивалентно, верхнюю оценку числа монет для данного сравнения).

Содержание раздела