Алгоритм Флойда нахождения кратчайших путей между парами вершин

Предположим, что мы имеем помеченный орграф, который содержит время полета по маршрутам, связывающим определенные города, и~мы хотим построить таблицу, где приводилось бы минимальное время перелета из одного (произвольного) города в любой другой. В этом случае мы сталкиваемся с общей задачей нахождения кратчайших путей, то есть нахождения кратчайших путей между всеми парами вершин орграфа.

Формулировка задачи.Есть ориентированный граф

, каждой дуге (ребру) этого графа сопоставлен неотрицательный вес . Общая задача нахождения кратчайших путей заключается в нахождении для каждой упорядоченной пары вершин

любого пути от вершины

в вершину

, длина которого минимальна среди всех возможных путей от

к

.

Можно решать эту задачу, последовательно применяя алгоритм Дейкстры для каждой вершины, объявляемой в качестве источника. Но мы для решения поставленной задачи воспользуемся алгоритмом, предложенным Флойдом (R.W. Floyd). Пусть все вершины орграфа последовательно пронумерованы от 1 до

. Алгоритм Флойда использует матрицу , в которой находятся длины кратчайших путей:

, если ;

, если ;

если отсутствует путь из вершины

в вершину

.

Над матрицей

выполняется итераций. После -й итерации содержит значение наименьшей длины пути из вершины в вершину , причем путь не проходит через вершины с номерами большими .

Вычисление на

-ой итерации выполняется по формуле:

Верхний индекс

обозначает значение матрицы

после

-ой итерации.

Для вычисления

проводится сравнение величины (то есть стоимость пути от вершины к вершине без участия вершины или другой вершины с более высоким номером) с величиной (стоимость пути от вершины к вершине плюс стоимость пути от вершины до вершины ). Если путь через вершину дешевле, чем , то величина

изменяется. Рассмотрим орграф:

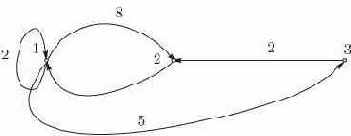
Рис. 16.1.  Помеченный орграф

Матрица A(3 * 3) на нулевой итерации (k = 0)

Матрица A(3 * 3) после первой итерации (k = 1)

Матрица A(3 * 3) после второй итерации (k = 2)

Матрица A(3 * 3) после третьей итерации (k = 3)

Содержание раздела

---

---