Внутренняя сортировка

Существует по крайней мере пять широких классов алгоритмов внутренней сортировки.

1. Вставка. На
   
   -м этапе
   
   -е имя помещается на надлежащее место между
   

   уже отсортированным именами:

1. Обмен. Два имени, расположение которых не соответствует порядку, меняются местами (обмен). Эти процедуры повторяются до тех пор, пока остаются такие пары.

1. Выбор. На
   
   -м этапе из неотсортированных имен выбирается
   
   -е наибольшее (наименьшее) имя и помещается на соответствующее место.

1. Распределение. Имена распределяются по группам, и содержимое групп затем объединяется таким образом, чтобы частично отсортировать таблицу; процесс повторяется до тех пор, пока таблица не будет отсортирована полностью.
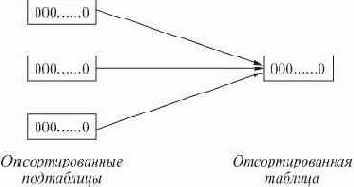
2. Слияние. Таблица делится на подтаблицы, которые сортируются по отдельности и затем сливаются в одну.

Эти классы нельзя назвать ни взаимоисключающими, ни исчерпывающими: одни алгоритмы сортировки можно с полным основанием отнести более чем к одному классу (пузырьковую сортировку можно рассматривать и как выбор, и как обмен), а другие не укладываются ни в один из классов. Тем не менее, перечисленные пять классов достаточно удобны для классификации обсуждаемых алгоритмов сортировки.

Сосредоточим внимание на первых четырех классах алгоритмов сортировки. Алгоритмы, основанные на слиянии, приемлемы для внутренней сортировки, но более естественно рассматривать их как методы внешней сортировки.

В описываемых алгоритмах сортировки имена образуют последовательность, которую будем обозначать

независимо от возможных пересылок данных; таким образом, значением является любое текущее имя в -й позиции последовательности. Многие алгоритмы сортировки наиболее применимы к массивам; в этом случае обозначает -й элемент массива. Другие алгоритмы более приспособлены для работы со связанными списками: здесь обозначает -й элемент списка. Следующие обозначения используются для пересылок данных:

значения и меняются местами.

значение присваивается имени .

значение имени присваивается .

Таким образом, операция

, которая встречается в различных алгоритмах сортировки, временно нарушает предположение о том, что никакие два имени не имеют одинаковых значений.
Однако это условие всегда обязательно восстанавливается.

В каждом из рассматриваемых алгоритмов будем считать, что имена нужно сортировать на месте. Другими словами, переразмещение имен должно происходить внутри последовательности ; при этом существуют одна или две дополнительные ячейки, в которых временно размещается значение имени. Ограничение "на месте" основано на предположении, будто число имен настолько велико, что во время сортировки не допускается перенос их в другую область памяти. Если в распоряжении имеется память, достаточная для такого переноса, то некоторые из обсуждаемых алгоритмов можно значительно ускорить. Эти рассмотрения заставляют нас в алгоритмах распределяющей сортировки и сортировки слиянием реализовать последовательность как связанный список.


Содержание раздела

---

---