Обменная сортировка

Обменная сортировка некоторым систематическим образом меняет местами пары имен, не отвечающие порядку, до тех пор, пока такие пары существуют. Фактически алгоритм 14.1 можно рассматривать как обменную сортировку, в которой имя

меняется местами со своим соседом слева, пока не оказывается на правильном месте. В этом разделе мы обсуждаем два типа обменных сортировок: хорошо известную, но относительно неэффективную пузырьковую сортировку и быструю сортировку — один из лучших со всех точек зрения алгоритмов внутренней сортировки.

Пузырьковая сортировка. Наиболее очевидный метод систематического обмена местами имен с неправильным порядком состоит в просмотре пар смежных имен последовательно слева направо и перемене мест тех имен, которые не отвечают порядку.

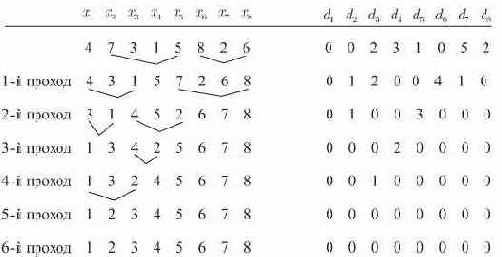
Рис. 14.2.  Пузырьковая сортировка, примененная к таблице. Показан вектор инверсии таблицы после каждого прохода

Эта техника получила название пузырьковой сортировки, так как большие имена "пузырьками всплывают" вверх (то есть на правый конец) таблицы. В алгоритме 14.2 эта простая идея реализуется с одним небольшим усовершенствованием: ясно, что не имеет смысла продолжать просмотр для больших имен (в правом конце таблицы), про которые известно, что они находятся на своих окончательных позициях. В алгоритме 14.2 используется переменная

, значение которой в начале цикла

равно наибольшему индексу

, такому, что про имя еще не известно, стоит ли оно в окончательной позиции. На рис. 14.2 показана работа алгоритма на примере таблицы с именами.

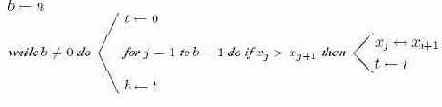
Алгоритм 14.2. Пузырьковая сортировка

Анализ пузырьковой сортировки зависит от трех факторов: числа проходов (то есть числа выполнений тела цикла

), числа сравнений и числа обменов . Число обменов равно, как в алгоритме 14.1, числу инверсий: 0 в лучшем случае, в худшем случае и - в среднем. Рисунок 14.2

дает возможность предположить, что каждый проход пузырьковой сортировки, исключая последний, уменьшает на единицу каждый ненулевой элемент вектора инверсий и циклически сдвигает вектор на одну позицию влево; легко доказать, что это верно в общем случае, и поэтому число проходов равно единице плюс наибольший элемент вектора инверсий. В лучшем случае имеется всего один проход, в худшем случае -

проходов и в среднем - проходов, где - вероятность того, что наибольшим элементом вектора инверсии является . Общее число сравнений имен трудно определить, но можно показать, что оно равно в лучшем случае, в худшем случае и - в среднем.

Пузырьковую сортировку можно несколько улучшить, но при этом она все еще не сможет конкурировать с более эффективными алгоритмами сортировки. Ее единственным преимуществом является простота.

Как в простой сортировке вставками, так и в пузырьковой сортировке (алгоритм 14.2) основной причиной неэффективности является тот факт, что обмены дают слишком малый эффект, так как в каждый момент времени имена сдвигаются только на одну позицию. Такие алгоритмы непременно требуют порядка

операций, как в среднем, так и в худшем случаях.

Быстрая сортировка. Идея метода быстрой сортировки состоит в том, чтобы выбрать одно из имен в таблице и использовать его для разделения таблицы на две подтаблицы, составленные соответственно из имен меньших и больших выбранного, которые затем рекурсивно сортируются с использованием быстрой сортировки. Разделение можно реализовать, одновременно просматривая таблицу и слева направо, и справа налево, меняя местами имена в неправильных частях таблицы. Имя, используемое для расщепления таблицы, затем помещается между двумя подтаблицами, и две подтаблицы сортируются рекурсивно.

В алгоритме 14.3 показаны детали быстрой сортировки для сортировки таблицы

, где

используется для разбиения таблицы на подтаблицы. На рис. 14.3 показано, как алгоритм 14.3 использует два указателя

и для просмотра таблицы во время разбиения. В начале цикла " " и указывают соответственно на первое и последнее имена, о которых известно, что они находятся не в тех частях файла, в которых требуется. Когда

встречаются, то есть когда

, все имена находятся в соответствующих частях таблицы и помещается между двумя частями, меняясь при этом местами с , алгоритм предполагает, что имя определено и больше, чем .

Алгоритм 14.3. Рекурсивный вариант быстрой сортировки, использующий первое имя для расщепления таблицы. Предполагается, что имя

определено и больше или равно

"

Рис. 14.3.  Фаза разбиения быстрой сортировки, использующей первое имя для разбиения таблицы. Значение не показано, оно предполагается большим, чем другие показанные значения

Алгоритм 14.3 изящен, но непрактичен. Проблема состоит в том, что рекурсия используется для записи подтаблиц, которые рассматриваются на более поздних этапах, и в худших случаях (когда таблица уже отсортирована) глубина рекурсии может равняться

. Следовательно, для стека, реализующего рекурсию, необходима память, пропорциональная ; для больших такое требование становится неприемлемым. Кроме того, второе рекурсивное обращение к быстрой сортировке в алгоритме 14.3 может быть легко исключено. По этим причинам мы предлагаем алгоритм 14.4, итерационный вариант быстрой сортировки, в которой стек ведется явно. Элементом стека является пара : когда пара находится в стеке, это значит, что нужно сортировать соответствующие . Алгоритм 14.4 помещает в стеке большую из двух подтаблиц и немедленно применяет алгоритм к меньшей подтаблице. Это уменьшает глубину стека в худшем случае примерно до . Заметим, что подтаблицы длины 1 игнорируются и что расщепление подтаблицы делается с использованием случайно выбранного имени в этой подтаблице.

увеличить изображение
Алгоритм 14.4.Итерационный вариант быстрой сортировки

Содержание раздела

---

---