Оптимальные деревья бинарного поиска

Бинарный поиск в последовательно распределенной таблице ( алгоритм 13.4.) обеспечивает очень быстрое нахождение имен, которые являются средними точками на раннем этапе процесса деления пополам, именно имен, близких к вершине дерева

. Таким образом, любое имя в таблице можно выбрать примерно за

сравнений.

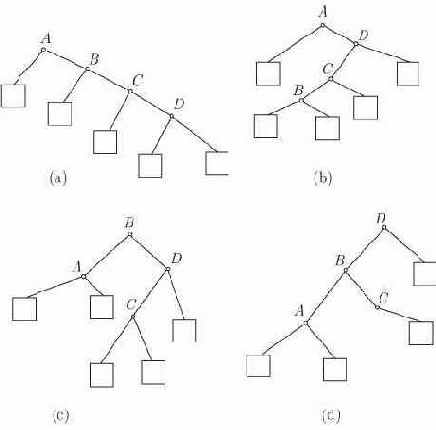
Рис. 13.1. Четыре дерева бинарного поиска над множеством имен {A,B,C,D}

На практике в большинстве таблиц встречаются имена, к которым обращаются гораздо чаще, чем к другим, и "привилегированные" места в таблице разумно постараться использовать для наиболее часто вызываемых имен, а не для имен, выбранных для этих мест в результате бинарного поиска. Это невозможно осуществить для последовательно распределенных таблиц, поскольку место имени определяется его положением относительно естественного порядка имен в таблице. Введем структуру данных, легко приспосабливаемую как к месту бинарного поиска, так и к возможности выделять точки, в которых таблица делится на две части.

Деревом бинарного поиска над именами

называется расширенное бинарное дерево, все внутренние узлы которого помечены различными именами из списка

таким образом, что симметричный порядок узлов совпадает с естественным порядком. Каждый из

внешних узлов соответствует промежутку в таблице. На рис. 13.1 показаны четыре различных дерева бинарного поиска на множестве имен

. Деревья (а) и (b) - вырожденные, поскольку они по существу являются линейными списками, которые должны просматриваться последовательно.

Поиск имени

в дереве бинарного поиска осуществляется путем сравнения

с именем, стоящим в корне. Тогда

Если корня нет (дерево пусто), то
в таблице отсутствует и поиск завершается безуспешно.
Если
совпадает с именем в корне, поиск завершается успешно.
Если
предшествует имени в корне, поиск продолжается ниже в левом поддереве корня.
Если
следует за именем в корне, поиск продолжается ниже в правом поддереве корня.

Пусть бинарное дерево имеет вид, в котором каждый узел представляет собой тройку (LEFT, NAME, RIGHT), где LEFT и RIGHTсодержат указатели левого и правого сыновей соответственно, и NAME содержит имя, хранящееся в узле.
Указатели могут иметь значение

, означающее, что поддерево, на которое они указывают пусто. Если указатель корня дерева есть

, то само дерево пусто. Как и следовало ожидать, успешный поиск завершается во внутреннем узле дерева бинарного поиска и безуспешный поиск завершается во внешнем узле.

Эта процедура нахождения имени

в таблице, организованная в виде дерева бинарного поиска

, показана в алгоритме 13.5. Отметим его сходство с алгоритмом 13.4 (бинарный поиск).

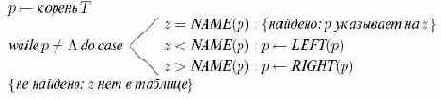
Алгоритм 13.5. Поиск в дереве бинарного поиска

Содержание раздела