Прохождения

Во многих приложениях необходимо пройти лес, заходя в узлы, то есть обрабатывая их некоторым систематическим образом. Посещение каждого узла может быть связано с простой операцией, такой как печать содержимого, или со сложной, такой как вычисление функции. Будем предполагать, что при посещении узла структура леса не меняется. Рассмотрим четыре основных способа прохождения леса: в глубину, снизу вверх, в горизонтальном порядке и для бинарных деревьев - в симметричном порядке.

При прохождении в глубину, известном также как прохождение в прямом порядке, узлы леса проходятся в соответствии со следующей рекурсивной процедурой:

1. Посетить корень первого дерева.
2. пройти в глубину поддерева первого дерева (если оно есть).
3. Пройти в глубину оставшиеся деревья, если они есть.

Например, для леса, показанного на рис. 4.7, узлы будут проходиться в следующем порядке:

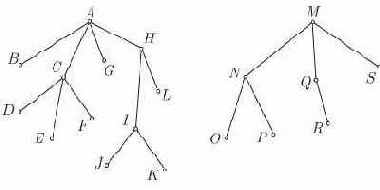
Рис. 4.7.  Лес

Название "в глубину" отражает тот факт, что после посещения некоторого узла мы продолжаем прохождение в глубь дерева всякий раз, когда это возможно. Такой порядок особенно полезен в процедурах поиска.

Для бинарных деревьев эта процедура упрощается и выглядит следующим образом.

1. Посетить корень.
2. Пройти в глубину левое поддерево
3. Пройти в глубину правое поддерево.

Прохождение снизу вверх, известное также как обратный порядок или концевой порядок, осуществляется согласно следующей рекурсивной процедуре:

• Пройти снизу вверх поддеревья первого дерева, если они есть.
• Посетить корень первого дерева.
• Пройти снизу вверх оставшиеся деревья, если они есть.

Название "снизу вверх" связано с тем, что в момент посещения произвольного узла его потомки оказываются уже пройденными. Такой порядок прохождения полезен, в частности, потому, что он позволяет вычислять рекурсивно определенные функции на лесах. При этом порядке прохождения узлы леса, показанного на рис. 4.7, проходятся в такой последовательности:

. Рекурсивная процедура прохождения снизу вверх применительно к бинарным деревьям имеет следующий вид:

1. Пройти снизу вверх левое дерево.
2. Пройти снизу вверх правое дерево.
3. Посетить корень.

Симметричный порядок для бинарных деревьев определяется рекурсивно следующим образом:

1. Пройти в симметричном порядке левое поддерево.
2. Посетить корень.
3. Пройти в симметричном порядке правое поддерево.

Такой способ прохождения известен также как лексикографический порядок или внутренний порядок. Заметим, что прохождение леса снизу вверх эквивалентно прохождению в симметричном порядке бинарного дерева, соответствующего этому лесу (при естественном соответствии).

Сравнивая рекурсивные процедуры прохождения бинарных деревьев в глубину, снизу вверх и в симметричном порядке, можно обнаружить их значительное сходство:

прохождение в глубинусимметричный порядокпрохождение снизу вверх

посетить корень	левое поддерево	левое поддерево
левое поддерево	посетить корень	правое поддерево
правое поддерево	правое поддерево	посетить корень

Это сходство позволяет построить общий нерекурсивный алгоритм, который может быть применен к каждому из этих порядков прохождения бинарных деревьев.

Горизонтальный порядок прохождения. При таком способе узлы леса проходятся слева направо, уровень за уровнем от корня вниз. Таким образом, в соответствии с этой процедурой узлы леса, показанного на рис.4.7, будут проходиться в следующем порядке: . Такое прохождение дерева полезно в определенных алгоритмах на графах.


Содержание раздела

---

---